Two Motors

This example code is an extension of onemotor.py. Its purpose is to show how to use list comprehensions to access and run the two motors. Note also that the current time (tcurr) will have different values for each motor. Using the correct time stamp for the sine wave value calculation will produce more accurate motion traces.

""" twomotors.py

Run two motors with a sinusoidal speed input.

Setup:
    Connect one large motor to port 'A'
    Connect one large motor to port 'B'

"""
# Importing modules and classes
import time
import numpy as np
from pyev3.utils import plot_line
from pyev3.brick import LegoEV3
from pyev3.devices import Motor

# Defining parameters (for two motors)
T = [2, 4]  # Period of sine wave (s)
u0 = [80, 60]  # Motor speed amplitude (%)
tstop = 2  # Sine wave duration (s)

# Pre-allocating output arrays
t = [[], []]
theta = [[], []]

# Creating LEGO EV3 objects
ports = ['A', 'B']
ev3 = LegoEV3()
motors = [Motor(ev3, port=port) for port in ports]

# Initializing motors
for motor in motors:
    motor.outputmode = 'power'
    motor.output = 0
    motor.reset_angle()
    motor.start()

# Initializing current time stamp and starting clock
tcurr = 0
tstart = time.perf_counter()
# Running motor sine wave output
while tcurr <= tstop:
    for i, motor  in enumerate(motors):
        # Getting current time (s)
        tcurr = time.perf_counter() - tstart
        # Assigning current motor sinusoidal
        # output using the current time stamp
        motor.output = u0[i] * np.sin((2*np.pi/T[i]) * tcurr)
        # Updating output arrays
        t[i].append(tcurr)
        theta[i].append(motor.angle)
# Stopping motors and closing brick connection
[motor.stop() for motor in motors]
ev3.close()

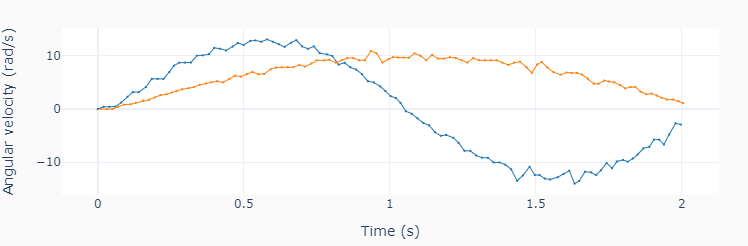
# Calculating motor angular velocity (rad/s)
w = []
for x, y in zip(t, theta):
    w.append(2*np.pi/360 * np.gradient(y, x))

# Plotting results
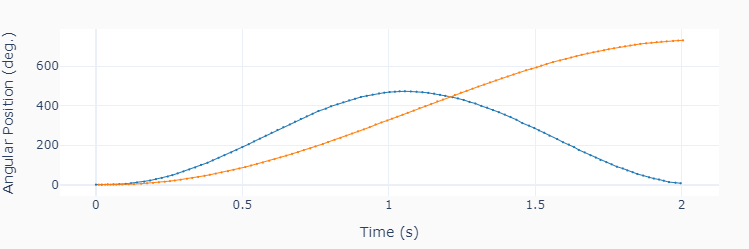
plot_line(t, theta, yname=['Angular Position (deg.)'], marker=True)
plot_line(t, w, yname=['Angular velocity (rad/s)'], marker=True)